C++ is a high-level object-oriented programming language with a faster run-time compared to most programming languages. This is because it is closer to machine language. Recent advancement in machine learning and other artificial intelligence-related facets have been implemented using Python due to its flexibility and rich library support as well as an active community of users.
C++ has a faster run-time when compared to other programming languages and thus is suitable for machine learning since fast and reliable feedback is essential in machine learning.
C++ also has rich library support that is used in machine learning, which we will get to later.
Goal
The goal of this tutorial is to educate you on how to implement machine learning algorithms using the C++ programming language. Since this is an introductory part, we will implement the algorithms from scratch to foster understanding. Afterwards it will be easier when we get started with libraries.
Prerequisites
To follow along this tutorial with ease, one should meet the following requirements.
- Have a basic understanding of programming in C++ and the use of objects in storing big data.
- A pre-installed IDE, preferably Codeblocks.
- A good mathematical background so as to understand the statistical methods to be used later on.
Machine learning definition
Machine learning is a facet of artificial intelligence. It refers to the ability of computer systems to independently find solutions to problems by recognizing patterns of data stored in a database. Humans are required to write the algorithms that are used by the computer system, collect data, and put it into datasets. Afterwards, the machine learns independently and can find solutions.
Implementation of the statistical and mathematical methods for machine learning in C++
Before we embark on writing the code, we need to understand the approach to be used. We will use a mathematical approach namely Linear regression to enable our system to learn.
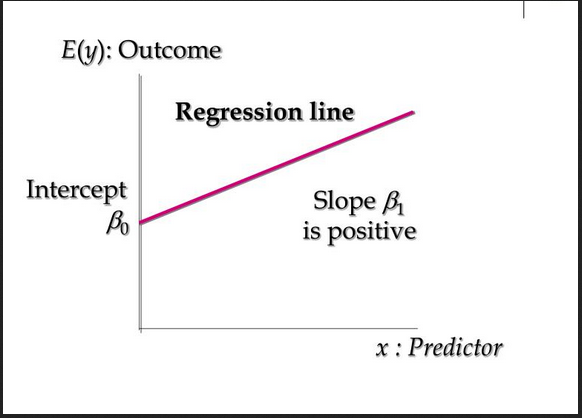
Linear regression
In Linear regression, we determine the value of a variable depending on the value of a second variable. The dependent variable is the variable whose value we are trying to calculate, while the independent variable is the value that helps us estimate the value of the dependent variable.
This can be expressed mathematically as shown below:
y=B0 + B1x
To put this into perspective, we can use linear regression to determine the amount of rainfall received in an area based on the temperature of the area. The dependent variable becomes the amount of rainfall received while the independent variable is temperature of the area.
Loss function
The error in what we predicted as the values of B0 and B1 is what is termed as the loss. We want to minimize the error so that we have the most accurate values for B0 and B1.
This gives us the best fit line that will then be used for more accurate predictions. The loss function used is as shown.
e^i=p^i- y^i
Whereby:
- e^i is the ith training example error.
- p^i is the ith training example predicted value.
- y^i is the ith training example real/actual value..
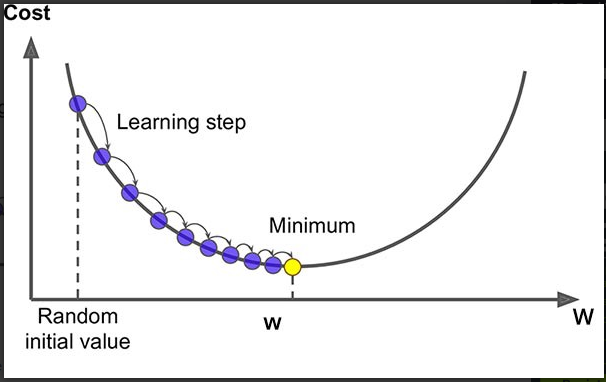
Algorithm for gradient descent
Gradient descent is a repetitive optimization algorithm useful when finding the minimum of a function, in our case, the loss function.
Let’s start with initialized values for B0 andB1 and basing on the error we get in each instance, we will update their value.
This is how it plays out: We start with the values B1 = 0 and B0 = 0. L will be the rate of learning. It controls how much B1 changes per step. For greater accuracy L could be made as small as possible. For example use 0.01 for good accuracy.
Proceed to calculate the error of the first point as follows: e(1) = p(1) – y(1)
Update the values for B0 and B1 based on the equations:
b0(t+1) = b0(t) - L * error
b1(t+1) = b1(t) - L * error
Do this operation for each training set instance. One epoch is completed this way. We repeat this for more epochs as required in order to obtain the least erroneous predictions possible.
Listed below are some references to better understand linear regression and gradient descent:
Implementing linear regression using C++
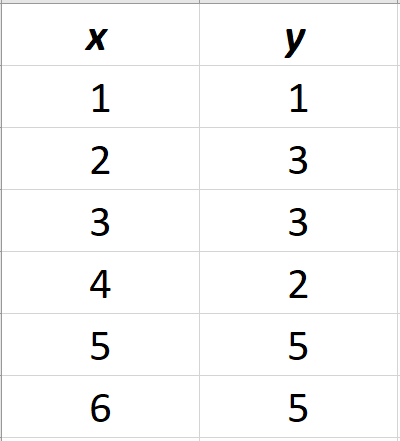
Let’s define the dataset that we will be using for our tutorial.
It’s contained in the image below:
We will use the first 5 values to train our algorithm and test it on the last value to see its performance:
double x[] = {1, 2, 3, 4, 5};
double y[] = {1, 3, 3, 2, 5};
Next, we’ll define our variables:
vector<double>error; // for storing the error values
double devi; // for calculating error on each stage,we name it devi(short for deviation) to differentiate it from the error vector
double b0 = 0; // initializing b0
double b1 = 0; // initializing b1
double learnRate = 0.01; // initializing our learning rate
Training Phase
Next, we will work on the gradient descent algorithm:
for (int i = 0; i < 20; i ++) { // Since there are five values and four epochs are needed, run a for loop 20 times.
int index = i % 5; // for accessing index after every epoch
double p = b0 + b1 * x[index]; // calculating prediction
devi = p - y[index]; // calculating error.
b0 = b0 - learnRate * devi; // updating b0
b1 = b1 - learnRate * devi * x[index];// updating b1
cout<<"B0="<<b0<<" "<<"B1="<<b1<<" "<<"error="<<devi<<endl; // printing values after every update
error.push_back(devi);
}
We use a for loop that runs 20 times since we are working with 5 values and the whole algorithm runs for 4 epochs. The expected value of each instance is calculated with the variable p. The error for each instance is stored in the variable devi according to the error equation we had listed above.
Variables b0 and b1 are then updated explained using the gradient descent algorithm. The error is pushed into the error vector.
Something worth noting is that
B0does not have any input. It is known as the bias or theyintercept and we assume it to have a fixed input value of 1.0. This assumption is helpful when implementing algorithm say when using arrays or vectors.
When finalizing, the error vector is sorted to obtain the lowest value of error and, as a result, the corresponding values of b0 and b1. We define a customized sorting function to sort the error vector.
Read about custom sorting in vectors here.
We’ll print the values:
sort(error.begin(),error.end(),custom_sort);// sorting to find the smallest value.
cout<<"Optimal end values are: "<<"B0="<<b0<<" "<<"B1="<<b1<<" "<<"error="<<error[0];
Testing :
cout<<"Enter a test x value";
double test;
cin>>test;
double pred=b0+b1*test;
cout<<"The value predicted by the model= "<<pred;
To test whether our algorithm is working, we enter 6 which is our test value. We get 4.9753 which is approximately equal to 5 when rounded off.
Congratulations! We have implemented a linear regression model in C++, and with good parameters.
The full code is shown below for implementation:
#include<bits/stdc++.h> // This header file contains all C++ libraries
using namespace std; // stdout library for printing values
bool custom_sort(double a, double b) /* this custom sort function sorts based on the minimum absolute value */
{
double a1=abs(a-0);
double b1=abs(b-0);
return a1<b1;
}
int main()
{
/*Intialization Phase*/
double x[] = {1, 2, 3, 4, 5}; // defining x values
double y[] = {1, 3, 3, 2, 5}; // defining y values
vector<double>error; // array to store all error values
double devi;
double b0 = 0; //initializing b0
double b1 = 0; //initializing b1
double learnRate = 0.01; //initializing error rate
/*Training Phase*/
for (int i = 0; i < 20; i ++) { // Since there are five values and four epochs are needed, run a for loop 20 times.
int index = i % 5; // This accesses the index after each epoch
double p = b0 + b1 * x[index]; // calculating prediction
devi = p - y[index]; // calculating error
b0 = b0 - learnRate * devi; // updating b0
b1 = b1 - learnRate * devi * x[index];// updating b1
cout<<"B0="<<b0<<" "<<"B1="<<b1<<" "<<"error="<<devi<<endl;// printing values after every update
error.push_back(devi);
}
sort(error.begin(),error.end(),custom_sort); // error values used to sort the data
cout<<"Optimal end values are: "<<"B0="<<b0<<" "<<"B1="<<b1<<" "<<"error="<<error[0]<<endl;
/*Testing Phase*/
cout<<"Enter a test x value";
double test;
cin>>test;
double pred=b0+b1*test;
cout<<endl;
cout<<"The value predicted by the model= "<<pred;
}
Conclusion
C++ is a good programming language for venturing into machine learning. However, since this is relatively new, you will have to implement most of the algorithms from scratch.
It would be difficult to implement machine learning in C++ without understanding the basics of machine learning algorithms. I think that is why Python is more popular for machine learning compared to C++.
C++ also has fewer libraries which support machine learning. We will go through libraries in a future article.
Linear regression in machine learning is useful for forecasting since the algorithm is able to make predictions based on previous patterns. This enables organizations and institutions to put in place strategies that are beneficial depending on the forecast.
Machine learning can also help small business determine the impact on their sales by altering various factors. This ensures that they carry out operations which bring in profit.
Machine learning also cuts the cost of human labor, that might take days to analyse data before giving you feasibility reports which may be prone to errors.
Happy coding!









Comments: